안녕하십니까.
최근 우연히 이기두 선생의 '각의 삼등분 이론'에 관한 글을 읽어보았습니다.
사실 이 선생은?각의 n등분의 작도가?가능하다?주장하신 것으로 알고 있는데, 그 주장이 타당하게 성립하려면 우선 '삼등분'에 관한 증명이 먼저 되어야 마땅할 것입니다.
그렇다면 이 선생의 이론이 타당한지 보도록 하겠습니다.
이 글을 읽기 전에 이기두 선생이 작성하신 '각의 삼등분 이론'을 먼저 읽고 오시는 것을 추천합니다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
이기두 선생은 '원호의 등분이 곧 각의 등분'이라는 간단한 정리를 응용하여 각의 삼등분 작도를 시도했다고 생각됩니다.
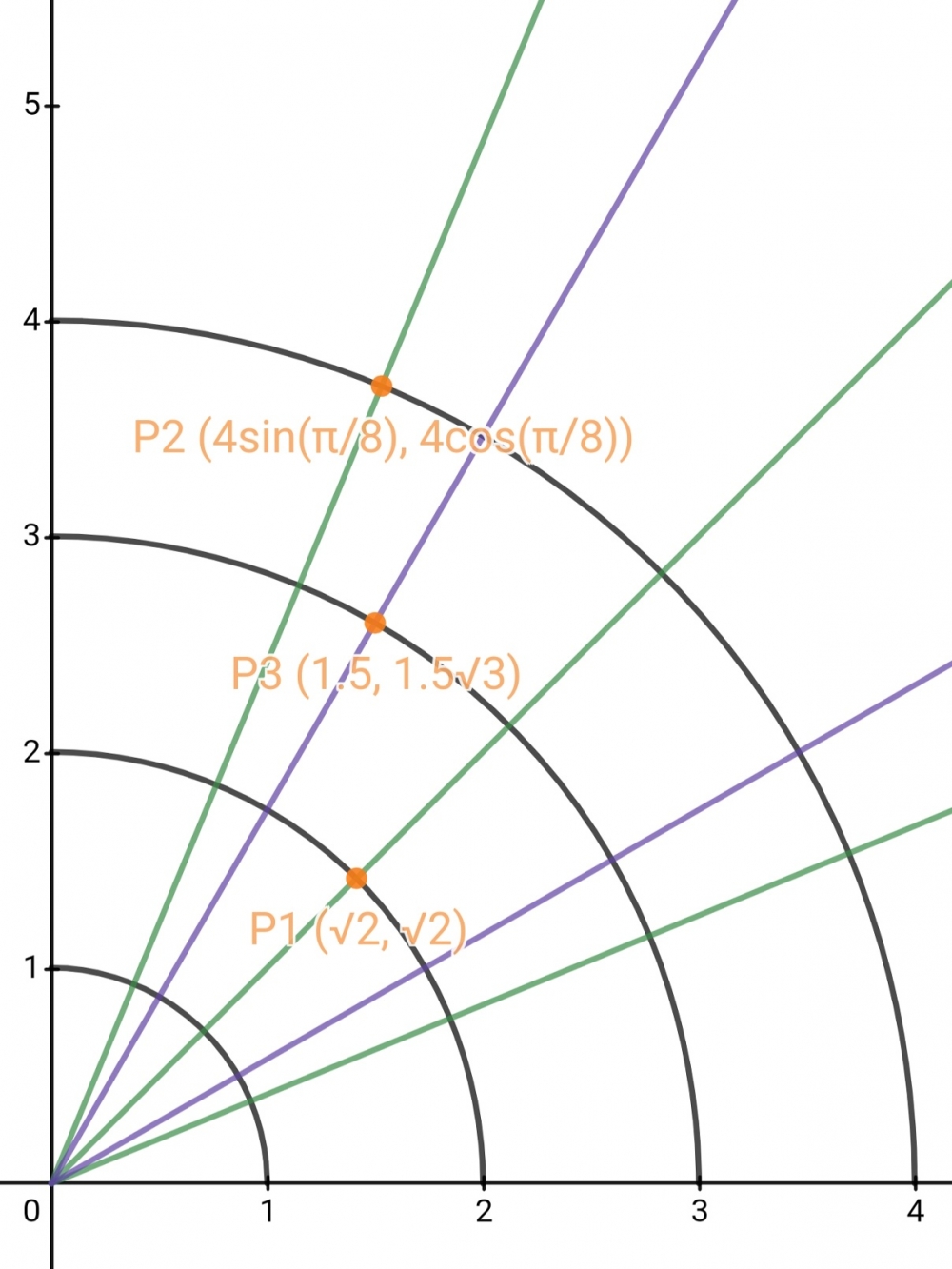
우선 이 선생의 주장을 요약하여 설명해 보겠습니다. 아래 그림을 참조하십시오.
1. 임의의 각을 정한다.
2. 이 각을 4등분하는 선을 그린다. 기울기가 작은 순서대로 L1, L2, L3이라 한다. 초록색 직선으로 나타내었습니다.
3. 반지름이 각각 1, 2, 3, 4인 원을 그린다. 반지름이 작은 순서대로 R1, R2, R3, R4라 한다. 검정색 곡선으로 나타내었습니다.
4. 원 R2와 직선 L2의 교점을 P1이라?한다. 원 R4와 직선 L3의 교점을 P2라 한다.
5. P1과 P2를 이어 선을 그리고, 그 선과 원 R3이 만나는 교점을 P3이라 한다.
6. 원점과 P3를 잇는다. 이 선은 주어진 각을 3등분하는 선이 된다.
하나씩 보도록 하겠습니다.
1. 아무 각이나 정하는 것이므로 직각 역시?될 것입니다.
? ?이 경우 각을 이루는 두 직선은?x=0, y=0이 됩니다.
2. 각의 사등분선의 식은 다음과 같습니다.
? ?L1: y=(√2-1)x
? ?L2: y=x
? ?L3: y=(√2+1)x
3. 원의 방정식은 다음과 같습니다.
? ?R1: x²+y²=1
? ?R2: x²+y²=4
? ?R3: x²+y²=9
? ?R4: x²+y²=16
4.?P1은?R2와 L2 즉?x²+y²=4와?y=x의 교점입니다.
? ?P2는?R4와 L3?즉?x²+y²=16과?y=(√2+1)x의 교점입니다.
? ?좌표는 다음과 같습니다.
? ?P1 (√2,?√2)
? ?P2 (4sin(π/8), 4cos(π/8))
5번에서 중요합니다. 5번으로 넘어가기 전에 그림을 잘 봅시다.
그림을 잘 보면, 이기두 선생의 원본 그림에는 없던 보라색 선이 추가되었습니다.
이 보라색 선은 직각을 3등분하는 선입니다.
선의 방정식은 다음과 같습니다.
y=√3 x
y=(1/√3)x
선생의 이론대로라면, 점 P3는 '원 R3 위의 점'이면서, 동시에 '각의 삼등분선 위에 있는 점'입니다.
따라서 이 선생이 말씀하시는 P3가 있다면, 그것은 반드시?R3: x²+y²=9와??y=√3?x의 교점이 될 것입니다.그 점의 좌표는 (1.5, 1.5√3)입니다.
여기서 다시?5번으로 들어갑니다. 5번에서 중요한 것은 P1, P2, P3가 모두 한 직선 상에 있다는 것입니다.
저 세 점의 좌표를 찍고 실제로 그으면, 과연 그럴까요?
저 세 점이 한 직선 상에 있다면 선생의 이론은 맞는 것이고, 아니라면 틀린 것이 되겠지요.
궁금하신 분들는 직접 해보기 바랍니다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
이기두 선생은 글을 올려 본인의 이론에 오류가 있었다고 인정하였습니다. 그리고 오류가 없이 완벽하다고 하는 새로운 이론을 들고 옵니다.
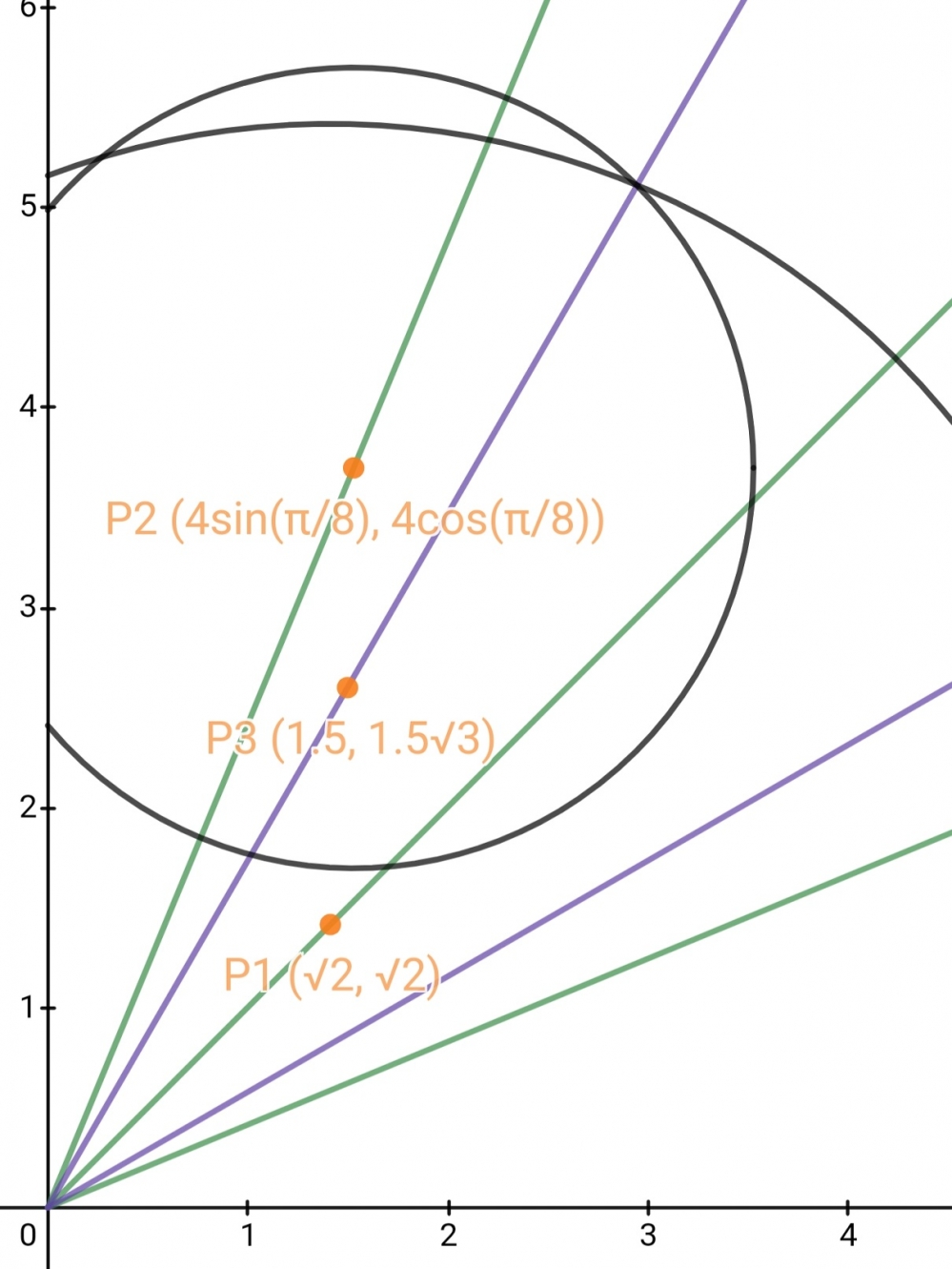
그것이 타당한지 또한 보겠습니다. 아래 그림을 참조하십시오,
6. P1을 중심으로 하고, R4와 반지름의 길이가?같은 원을 그린다.
7. P2를 중심으로 하고, R2와 반지름의 길이가 같은 원을 그린다.
8. 새로 그린 두 원의 교점을 P4라 한다.
9. 원점과 P4를 잇는다. 이 선은 주어진 각을 3등분하는 선이 된다.
하나씩 보도록 하겠습니다.
6. P1 (√2,?√2)를 중심으로 하고 반지름이 4인 원의 방정식은
? ?(x-√2)²+(y-√2)²=16
7.?P2 (4sin(π/8), 4cos(π/8))를 중심으로 하고 반지름이 2인 원의 방정식은
? ?(x-4sin(π/8))²+(y-4cos(π/8)²=4
8. 두 원의 교점은 참값을 구하기가 거의 불가능에 가깝습니다. 따라서 소수점 6자리에서 반올림한 근사값을 쓰도록 하겠습니다.
? ?궁금하신 분들은 직접 구해보시기 바랍니다.
? ?두 원의 교점 P4 (2.99495, 5.10973)
9. 이제 마지막입니다. 이 점 P4가 직선?y=√3?x 위에 있으면 이기두 선생의 이론은 맞는 것입니다.
? ?y좌표를 x좌표로 나누면?√3이 나오는지 보면 됩니다. 매우 쉬운 일입니다.
? ?5.10973/2.99495=1.70612
? ?√3=1.73205
? ?오차가 좀 있는 것 같군요. 얼마나 되는지 구해 봅시다.
? ?(√3-1.70612)/√3=1.49712%
? ?대략 1.5%의 오차를 보입니다. 소수점 5자리 근사치를 쓴 것 치고는 오차가 꽤 많이 나오는 것 같지 않습니까?
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
여기서 얻을 수 있는 결론은 두 가지로 나뉩니다.
1. 이기두 선생의 이론은 틀렸다.
2. 이기두 선생의 이론은 직각에 한해서만 적용되지 않는 것이다. 실제 이 선생의 이론에서 쓰인 각은 직각보다 작기 때문이다.
이기두 선생을 비롯한 여러분의 의견은 어떠한지 알고 싶습니다.
